树(Tree)是最重要的数据结构之一,它是由
n
(
n
∈
N
)
n(n \in \mathbb{N})n(n∈N) 个节点(也会被写作“结点”)构成的一个集合。其具有层次关系。树是递归定义的。
如下图,这就是一棵普通的树。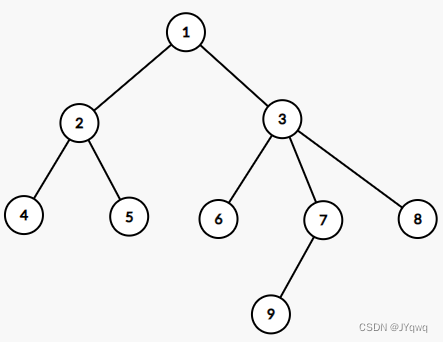
- 最上面的
1
1
1 称为根节点,最下面的4
,
5
,
6
,
9
,
8
4,5,6,9,8
4,5,6,9,8 称为叶子节点。 - 每两个节点之间相连线的称为边。
-
1
1
1 的下方与其相连的有2
,
3
2,3
2,3,我们就说,节点1
1
1 是2
,
3
2,3
2,3 的父节点(父亲),2
,
3
2,3
2,3 是1
1
1 的子节点(儿子),2
,
3
2,3
2,3 互为兄弟节点。 - 节点
9
9
9 的父亲是7
7
7,7
7
7 的父亲是3
3
3,3
3
3 的父亲是1
1
1。我们认为,1
,
3
,
7
1,3,7
1,3,7 是9
9
9 的祖先,3
,
7
,
9
3,7,9
3,7,9 是1
1
1 的子孙。 - 节点
1
1
1 有2
2
2 个子节点,我们认为,节点1
1
1 的度是2
2
2。叶子结点的度为0
0
0。 - 度不为零的(非叶子节点)节点称为分支节点。
- 一棵树的层数称为树的深度/树的高度。单独的根节点深度为
0
0
0 或1
1
1。图示的树的深度为3
3
3 或4
4
4。 - 空集合也是树,称为空树。其没有节点。
- 假如去掉了根节点,可以发现,就形成了一棵根节点为
2
2
2 的树,一棵根节点为3
3
3 的树。我们认为这两棵树是根节点为1
1
1 的树的子树。假如这两棵树属于同一集合且不相交,我们就说这个集合时森林。
- 一棵非空树有且只有一个根节点。
- 每一个非根节点有且只有一个父节点。
- 每一个叶子节点没有子节点。
- 一棵树有且只有
n
−
1
n-1
n−1 条边。
我们主要介绍其中两种。
3-1. 邻接矩阵
顾名思义,其是一个二维数组。
定义方式:
bool tree[N][N];
tree
i
,
j
\text{tree}_{i,j}treei,j 表示节点
i
,
j
i,ji,j 之间是否连通。
如果要将节点
u
uu 添加儿子
v
vv,那么操作就是tree[u][v]=1;。
将上图的树存储进去,就是这样的:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
访问所有节点的儿子:
for(int i=1;i<=n;i++)//n=9{ cout<<i<<": ";for(int j=1;j<=n;j++){if(tree[i][j]) cout<<j<<' ';}puts("");}输出:
1: 2 3 2: 4 5 3: 6 7 8 4: 5: 6: 7: 9 8: 9:邻接矩阵的优点:简洁明了,方便快捷;
邻接矩阵的缺点:浪费空间,容易被卡。
只建议数据中结点数
≤
8
×
1
0
3
\le 8\times 10^3≤8×103 时使用。
3-2. 邻接表
我们也可以采用其中一种叫做邻接表的常用存储方法。
定义方式:
vector<int>tree[N];在
tree
i
\text{tree}_itreei 的 vector 中,我们要存储什么呢?
没错,就是节点
i
ii 的儿子。
如果要将节点
u
uu 添加儿子
v
vv,那么操作就是tree[u].push_back(v);。
将上图的树存储进去,就是这样的:
| 节点编号 | 存储情况 |
|---|---|
| 1 | 2,3 |
| 2 | 4,5 |
| 3 | 6,7,8 |
| 4 | (空) |
| 5 | (空) |
| 6 | (空) |
| 7 | 9 |
| 8 | (空) |
| 9 | (空) |
如果要访问,也很简单(示例代码为访问上述树的儿子):
for(int i=1;i<=n;i++)//n=9{ cout<<i<<": ";for(auto j:tree[i]){ cout<<j<<' ';}puts("");}输出:
1: 2 3 2: 4 5 3: 6 7 8 4: 5: 6: 7: 9 8: 9:邻接表的优点在于:方便、省空间、速度较快,是通用的存储方法。
4-1. 先/前序(根)遍历(深度优先遍历)
先序遍历的遍历顺序是根→按序遍历子树。
类似于深度优先搜索,先序遍历就是一头猛扎到底,不到黄河不回头。
示例代码(输出树的先序遍历顺序):
voidpre(int p)//p 为当前节点编号{ cout<<p<<' ';for(auto i:tree[p]){pre(i);}}若为上面的树,则输出1 2 4 5 3 6 7 9 8。
4-2. 后序(根)遍历
后序遍历顺序和先序遍历相反,为按序遍历子树→根。
示例代码(输出树的后序遍历顺序):
voidpost(int p)//p 为当前节点编号{for(auto i:tree[p]){post(i);} cout<<p<<' ';//可以发现,只是改动了输出位置}若为上面的树,则输出4 5 2 6 9 7 8 3 1。
4-3. 层次遍历(宽/广度优先遍历)
层次遍历的写法类似广度优先搜索,使用队列存储节点,然后输出每一层的节点。
示例代码(输出树的层次遍历):
queue<int>q;voidbfs(){ q.push(root);//root 为根节点while(!q.empty()){int x=q.front(); q.pop(); cout<<x<<' ';for(auto i:tree[x]){ q.push(i);}}}若为上面的树,则输出1 2 3 4 5 6 7 8 9。
4-4. 叶子节点遍历
顾名思义,只遍历叶子节点,那我们随便写就可以了。
dfs 写法:
voiddfs(int p)//p 为当前节点编号{if(tree[p].empty()){ cout<<p<<' ';return;}for(auto i:tree[p]){pre(i);}}bfs 写法:
queue<int>q;voidbfs(){ q.push(root);//root 为根节点while(!q.empty()){int x=q.front(); q.pop();if(tree[x].empty()) cout<<x<<' ';else{for(auto i:tree[x]){ q.push(i);}}}}枚举写法:
for(int i=1;i<=n;i++)//n 为节点数{if(tree[i].empty()) cout<<i<<' ';}- 给定节点关系,输出先序、后序、层次、叶节点遍历的结果(根节点不一定是
1
1
1)。 - 给定节点关系,求树的深度。
- 给定节点关系,求出两个节点相距距离最长是多少(父子节点的边算一个单位长度)。
热门文章
- 动物疫苗作用是什么 动物疫苗作用是什么意思
- 猫咪能听懂人说话吗(猫咪能听懂人说话吗知乎)
- 2月8日|最高速度18.8M/S,2025最新Hysteria2免费节点高速订阅链接,便宜机场推荐
- 原生JS实现一个好看计数器
- 免费领养宠物的平台小狗是真的吗(免费领养宠物的平台小狗是真的吗知乎)
- 重庆猫咪领养微信群号(重庆猫网领养)
- 动物医院24小时全天候诊多少钱(动物医院一般几点关门)
- 1月16日|最高速度21.2M/S,2025最新Hysteria2免费节点高速订阅链接,便宜机场推荐
- 佳雯宠物医院客服电话是多少啊(佳雯宠物医院总部地址)
- 中国兽药厂家排名前100强有哪些 中国兽药厂家排名前100强有哪些品牌