什么是树表查询?
借助具有特殊性质的树数据结构进行关键字查找。
本文所涉及到的特殊结构性质的树包括:
二叉排序树。平衡二叉树。
使用上述树结构存储数据时,因其本身对结点之间的关系以及顺序有特殊要求,也得益于这种限制,在查询某一个结点时会带来性能上的优势和操作上的方便。
树表查询属于动态查找算法。
所谓动态查找,不仅仅能很方便查询到目标结点。而且可以根据需要添加、删除结点,而不影响树的整体结构,也不会影响数据的查询。
本文并不会深入讲解
树数据结构的基本的概念,仅是站在使用的角度说清楚动态查询。阅读此文之前,请预备一些树的基础知识。
1. 二叉排序树
二叉树是树结构中具有艳明特点的子类。
二叉树要求树的每一个结点(除叶结点)的子结点最多只能有2 个。在二叉树的基础上,继续对其进行有序限制则变成二叉排序树。
二叉排序树特点:
基于二叉树结构,从根结点开始,从上向下,每一个父结点的值大于左子结点(如果存在左子结点)的值,而小于右子结点(如果存在右子结点)的值。则把符合这种特征要求的树称为二叉排序树。
1.1 构建一棵二叉排序树
如有数列nums=[5,12,4,45,32,8,10,50,32,3]。通过下面流程,把每一个数字映射到二叉排序树的结点上。
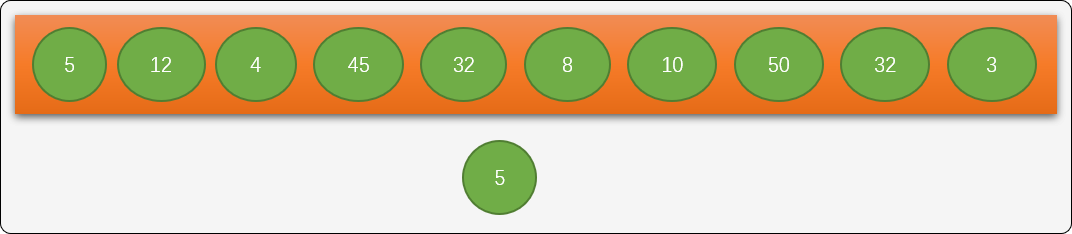
- 如果树为空,把第一个数字作为根结点。如下图,数字
5作为根结点。
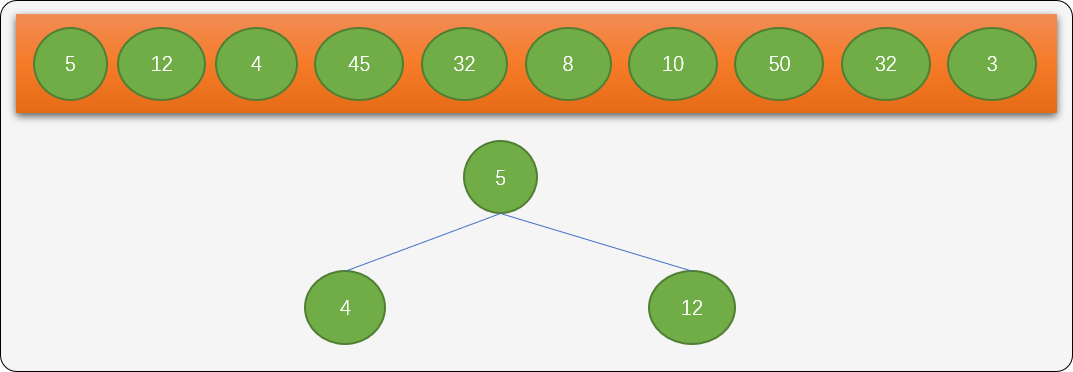
- 如果已经存在根结点,则把数字和根结点比较,小于根结点则作为根结点的左子结点,大于根结点的作为根结点的右子结点。如数字
4插入到左边,数字12插入到右边。
- 数列中后面的数字依据相同法则,分别插入到不同子的位置。
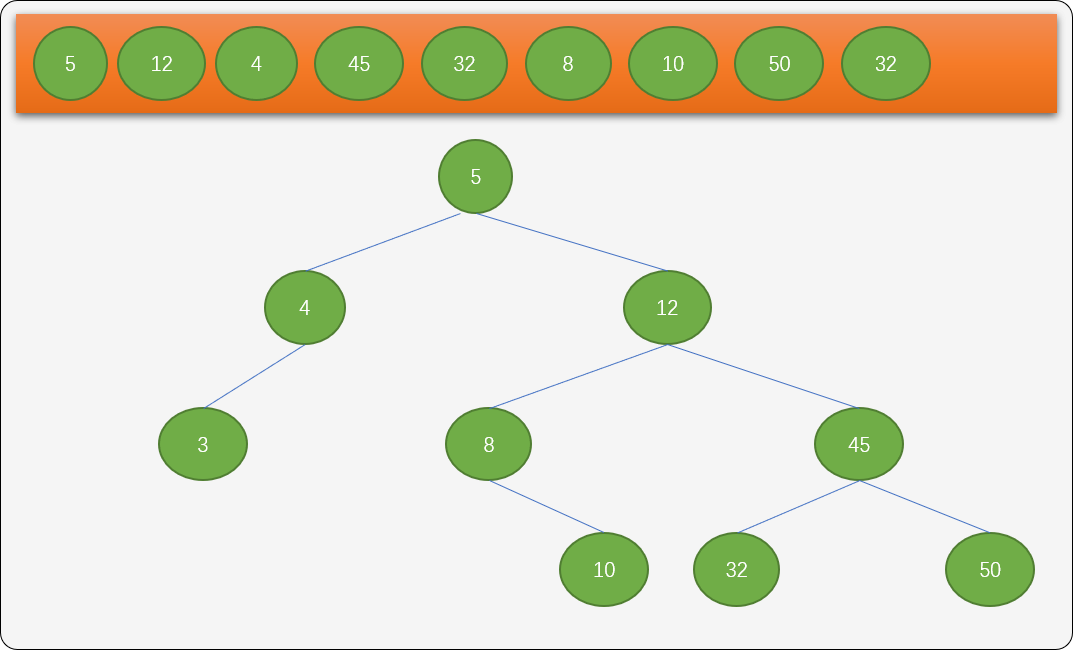
原始数列中的数字是无序的,根据二叉排序树的插入算法,最终可得到一棵有排序性质的树结构。对此棵树进行中序遍历就可得到从小到大的一个递增有序数列。
综观二叉排序树,进行关键字查找时,也应该是接近于二分查找算法的时间度。
这里有一个要注意的地方。
原始数列中的数字顺序不一样时,生成的二叉排序树的结构也会有差异性。对于查找算法的性能会产生影响。
1.2 二叉排序树的数据结构
现在使用OOP设计方案描述二叉排序树的数据结构。
首先,设计一个结点类,用来描述结点本身的信息。
''' 二叉排序树的结点类 ''' class TreeNode(): def __init__(self, value): # 结点上的值 self.value = value # 左结点 self.l_child = None # 右结点 self.r_child = None结点类中有3 个属性:
value:结点上附加的数据信息。l_child:左子结点,初始值为None。r_child:右子结点,初始值为None。
二叉排序树类: 用来实现树的增、删、改、查。
''' 二叉排序树类 ''' class BinarySortTree: # 初始化树 def __init__(self, value=None): pass ''' 在整棵树上查询是否存在给定的关键字 ''' def find(self, key): pass ''' 使用递归进行查询 ''' def find_dg(self, root, key): pass ''' 插入新结点 ''' def insert(self, value): pass ''' 中序遍历 ''' def inorder_traversal(self): pass ''' 删除结点 ''' def delete(self, key): pass ''' 检查是不是空树 ''' def is_empty(self): return self.root == None二叉排序树中可以有更多方法,本文只关注与查找主题有关的方法。
1.3 实现二叉排序树类中的方法:
__init__ 初始化方法:
# 初始化树 def __init__(self, value=None): self.root = None if value is not None: root_node = TreeNode(value) self.root = root_node在初始化树对象时,如果指定了数据信息,则创建有唯一结点的树,否则创建一个空树。
关键字查询方法:查询给定的关键字在二叉排序树结构中是否存在。
查询流程:
- 把给定的关键字和根结点相比较。如果相等,则返回查找成功,结束查询.
- 如果根结点的值大于关键字,则继续进入根结点的左子树中开始查找。
- 如果根结点的值小于关键字,则进入根结点的右子树中开始查找。
- 如果没有查询到关键字,则返回最后访问过的结点和查询不成功信息。
关键字查询的本质是二分思想,以当前结点为分界线,然后向左或向右进行分枝查找。
非递归实现查询方法:
''' 在整棵树上查询是否存在给定的关键字 key: 给定的关键字 ''' def find(self, key): # 从根结点开始查找。 move_node = self.root # 用来保存最后访问过的结点 last_node = None while move_node is not None: # 保存当前结点 last_node = move_node # 把关键字和当前结点相比较 if self.root.value == key: # 出口一:成功查找 return move_node elif move_node.value > key: # 在左结点查找 move_node = move_node.l_child else: # 在右结点中查找 move_node = move_node.r_child # 出口二:如果没有查询到,则返回最后访问过的结点及None(None 表示没查询到) return last_node, None注意:当没有查询到时,返回的值有
2个,最后访问的结点和没有查询到的信息。为什么要返回最后一次访问过的结点?
反过来想想,本来应该在这个地方找到,但是没有,如果改成插入操作,就应该插入到此位置。
基于递归实现的查找:
''' 使用递归进行查询 ''' def find_dg(self, root, key): # 结点不存在 if root is None: return None # 相等 if root.value == key: return root if root.value > key: return self.find_dg(root.l_child, key) else: return self.find_dg(root.r_child, key)再看看如何把数字插入到二叉排序树中,利用二叉排序树进行查找的前提条件就是要把数字映射到二叉排序树的结点上。
插入结点的流程:
- 当需要插入某一个结点时,先搜索是否已经存在于树结构中。
- 如果没有,则获取到查询时访问过的最一个结点,并和此结点比较大小。
- 如果比此结点大,则插入最后访问过结点的右子树位置。
- 如果比此结点小,则插入最后访问过结点的左子树位置。
insert 方法的实现:
''' 插入新结点 ''' def insert(self, value): # 查询是否存在此结点 res = self.find(value) if type(res) != TreeNode: # 没找到,获取查询时最后访问过的结点 last_node = res[0] # 创建新结点 new_node = TreeNode(value) # 最后访问的结点是根结点 if last_node is None: self.root = new_node if value > last_node.value: last_node.r_child = new_node else: last_node.l_child = new_node怎么检查插入的结点是符合二叉树特征?再看一下前面根据插入原则手工绘制的插入演示图:
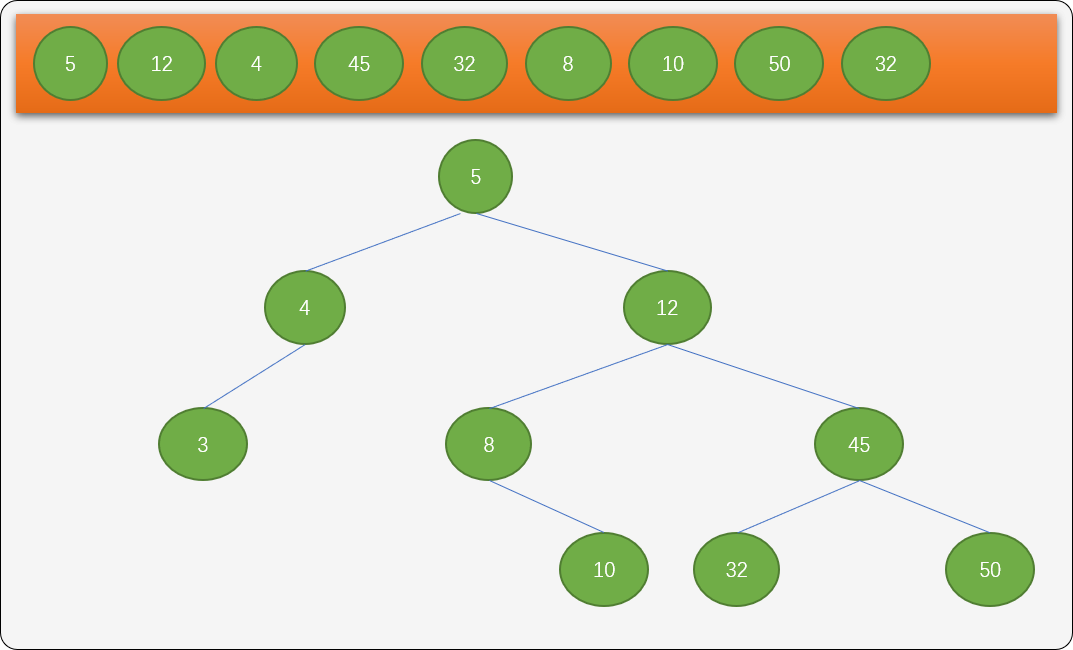
上图有4 个子结点,写几行代码测试一下,看从根结点到叶子结点的顺序是否正确。
测试插入方法:
if __name__ == "__main__": nums = [5, 12, 4, 45, 32, 8, 10, 50, 32, 3] tree = BinarySortTree(5) for i in range(1, len(nums)): tree.insert(nums[i]) print("测试根5 -> 左4 ->左3:") tmp_node = tree.root while tmp_node != None: print(tmp_node.value, end=" ->") tmp_node = tmp_node.l_child print("\n测试根5 -> 右12 ->右45->右50:") tmp_node = tree.root while tmp_node != None: print(tmp_node.value, end=" ->") tmp_node = tmp_node.r_child ''' 输出结果: 测试根5 -> 左4 ->左3: 5 ->4 ->3 -> 测试根5 -> 右12 ->右45->右50: 5 ->12 ->45 ->50 -> '''查看结果,可以初步判断插入的数据是符合二叉排序树特征的。当然,更科学的方式是写一个遍历方法。树的遍历方式有3 种:
- 前序:根,左,右。
- 中序:左,根,右。
- 后序。左,右,根。
对二叉排序树进行中序遍历,理论上输出的数字应该是有序的。这里写一个中序遍历,查看输出的结点是不是有序的,从而验证查询和插入方法的正确性。
使用递归实现中序遍历:
''' 中序遍历 ''' def inorder_traversal(self, root): if root is None: return self.inorder_traversal(root.l_child) print(root.value,end="->") self.inorder_traversal(root.r_child)测试插入的顺序:
if __name__ == "__main__": nums = [5, 12, 4, 45, 32, 8, 10, 50, 32, 3] tree = BinarySortTree(5) # res = tree.find(51) for i in range(1, len(nums)): tree.insert(nums[i]) tree.inorder_traversal(tree.root) ''' 输出结果 3->4->5->8->10->12->32->45->50-> '''二叉排序树很有特色的数据结构,利用其存储特性,可以很方便地进行查找、排序。并且随时可添加、删除结点,而不会影响排序和查找操作。基于树表的查询操作称为动态查找。
二叉排序树中如何删除结点
从二叉树中删除结点,需要保证整棵二叉排序树的有序性依然存在。删除操作比插入操作要复杂,下面分别讨论。
- 如果要删除的结点是叶子结点。
只需要把要删除结点的父结点的左结点或右结点的引用值设置为空就可以了。
- 删除的结点只有一个右子结点。如下图删除结点
8。
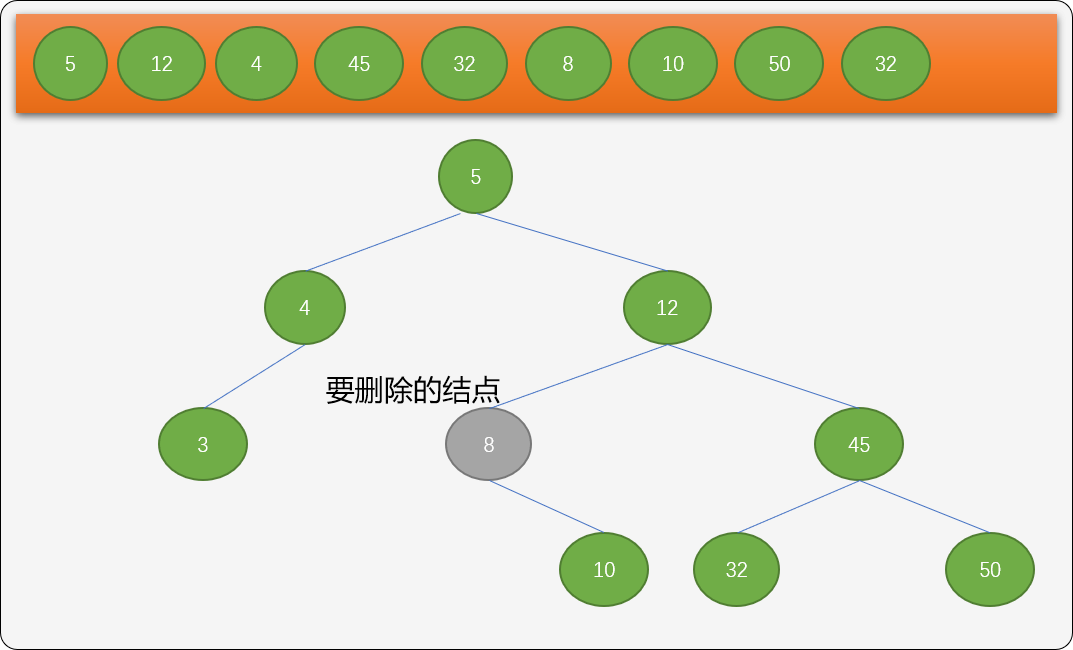
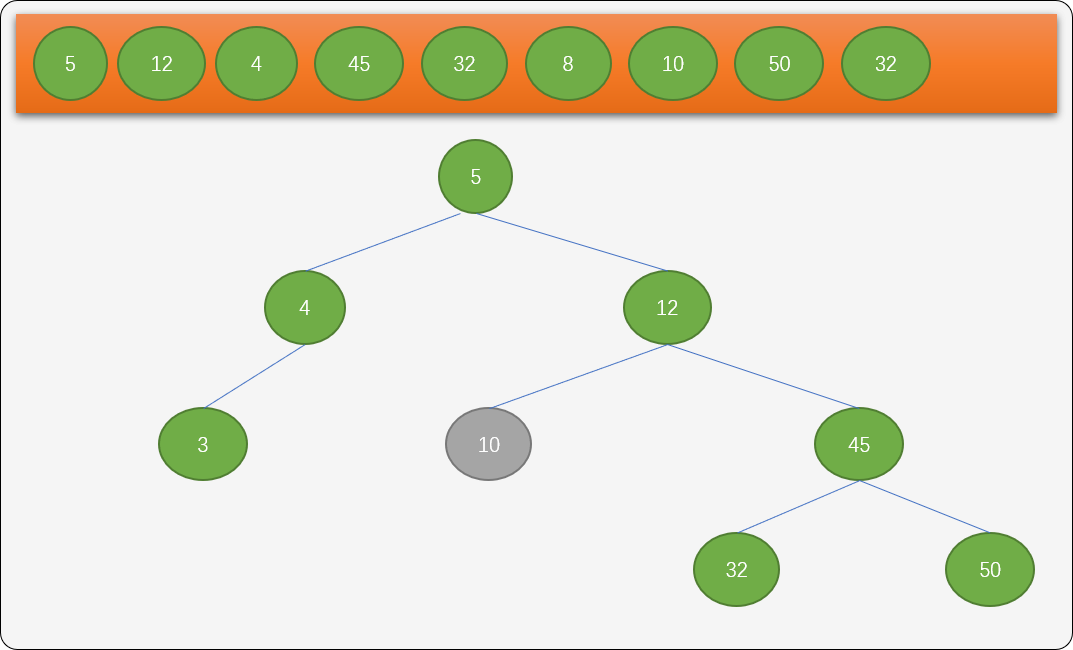
因为结点8没有左子树,在删除之后,只需要把它的右子结点替换删除结点就可以了。
- 删除的结点即存在左子结点,如下图删除值为
25的结点。
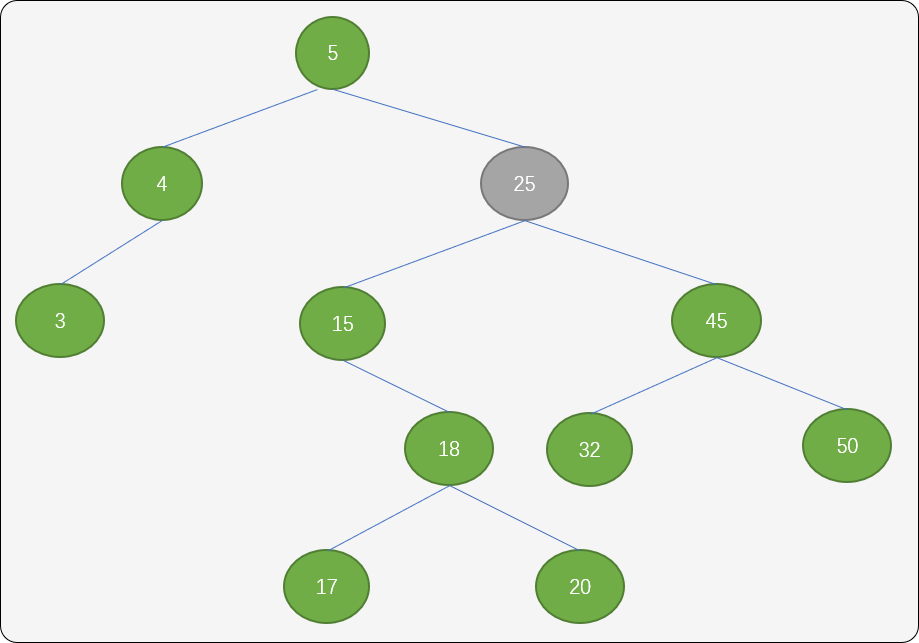
一种方案是:找到结点25 的左子树中的最大值,即结点20(该结点的特点是可能会存在左子结点,但一定不会有右子结点)。用此结点替换结点25 便可。
为什么要这么做?
道理很简单,既然是左子树中的最大值,替换删除结点后,整个二叉排序树的特性可以继续保持。
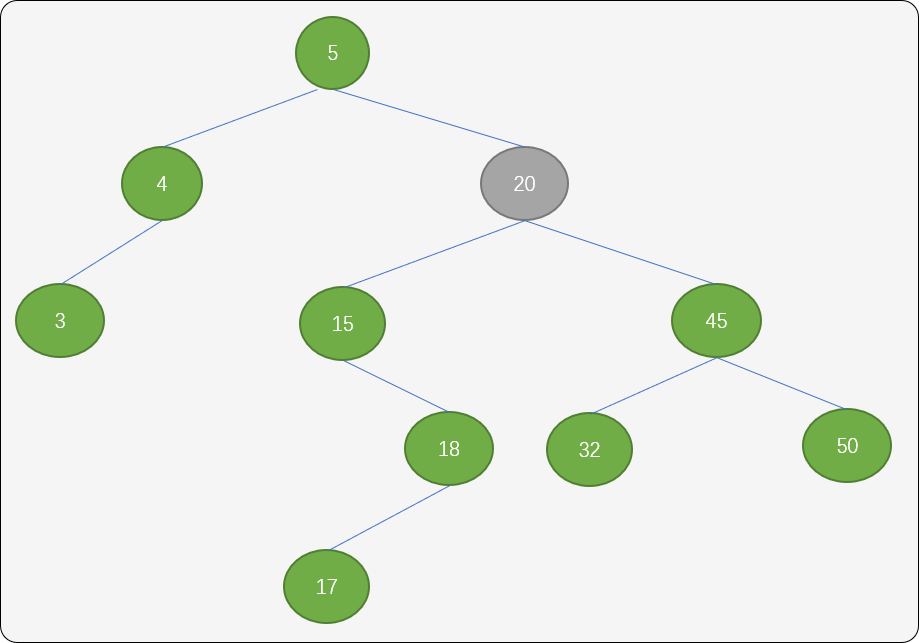
如果结点20 存在左子结点,则把它的左子结点作为结点18的右子结点。
另一种方案:同样找到结点25中左子树中的最大值结点20,然后把结点25 的右子树作为结点20 的右子树。
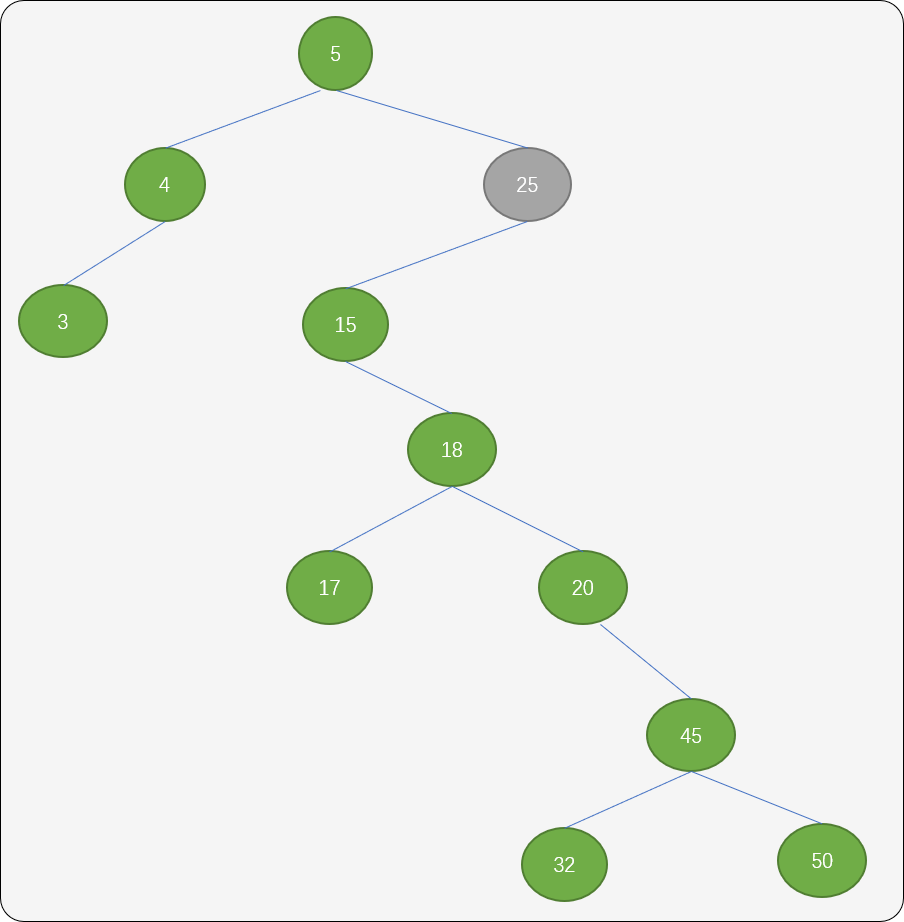
再把结点25 的左子树移到25 位置。
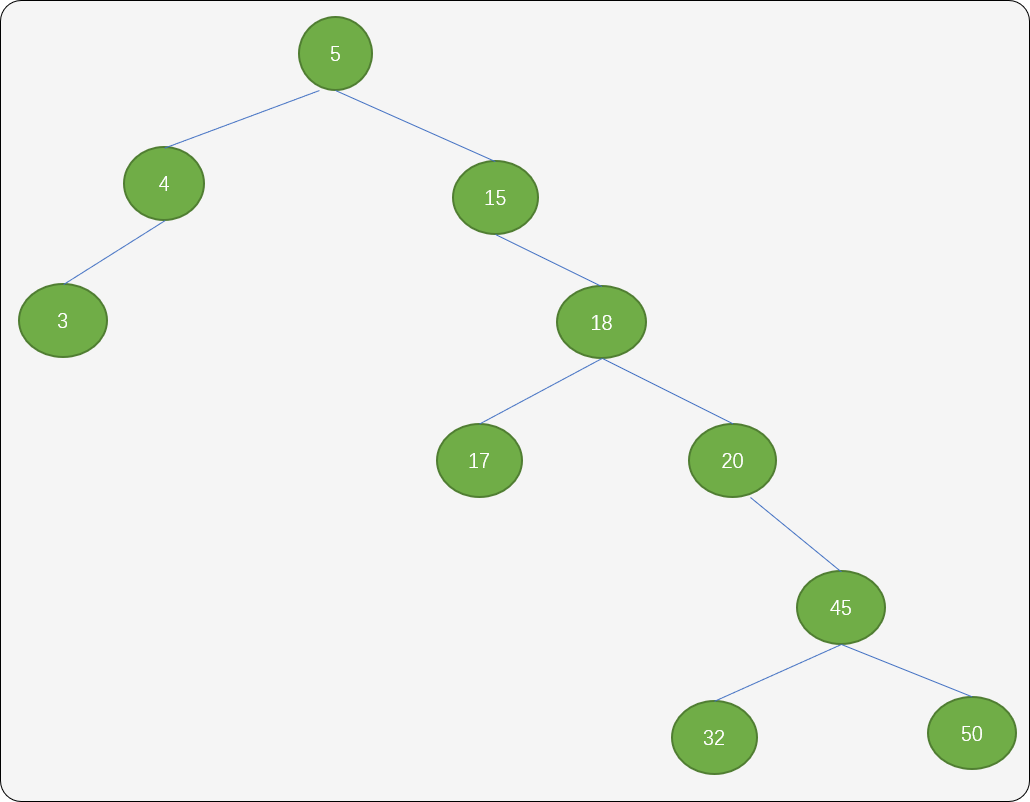
这种方案会让树增加树的深度。所以,建议使用第一种方案。
删除方法的实现:
''' 删除结点 key 为要要删除的结点 ''' def delete(self, key): # 从根结点开始查找,move_node 为搜索指针 move_node = self.root # 要删除的结点的父结点,因为根结点没有父结点,初始值为 None parent_node = None # 结点存在且没有匹配上要找的关键字 while move_node is not None and move_node.value != key: # 保证当前结点 parent_node = move_node if move_node.value > key: # 在左子树中继续查找 move_node = move_node.l_child else: # 在右子树中继续查找 move_node = move_node.r_child # 如果不存在 if move_node is None: return -1 # 检查要删除的结点是否存在左子结点 if move_node.l_child is None: if parent_node is None: # 如果要删除的结点是根结点 self.root = move_node.r_child elif parent_node.l_child == move_node: # 删除结点的右结点作为父结点的左结点 parent_node.l_child = move_node.r_child elif parent_node.r_child == move_node: parent_node.r_child = move_node.r_child return 1 else: # 如果删除的结点存在左子结点,则在左子树中查找最大值 s = move_node.l_child q = move_node while s.r_child is not None: q = s s = s.r_child if q == move_node: move_node.l_child = s.l_child else: q.r_child = s.l_child move_node.value = s.value q.r_child = None return 1测试删除后的二叉树是否依然维持其有序性。
if __name__ == "__main__": nums = [5, 12, 4, 45, 32, 8, 10, 50, 32, 3] tree = BinarySortTree(5) # res = tree.find(51) for i in range(1, len(nums)): tree.insert(nums[i]) tree.delete(12) tree.inorder_traversal(tree.root) ''' 输出结果 3->4->5->8->10->32->45->50-> '''无论删除哪一个结点,其二叉排序树的中序遍历结果都是有序的,很好地印证了删除算法的正确性。
3. 平衡二叉排序树
二叉排序树中进行查找时,其时间复杂度理论上接近二分算法的时间复杂度,其查找时间与树的深度有关。但是,这里有一个问题,前面讨论过,如果数列中的数字顺序不一样时,所构建出来的二叉排序树的深度会有差异性,对最后评估时间性能也会有影响。
如有数列[36,45,67,28,20,40]构建的二叉排序树如下图:
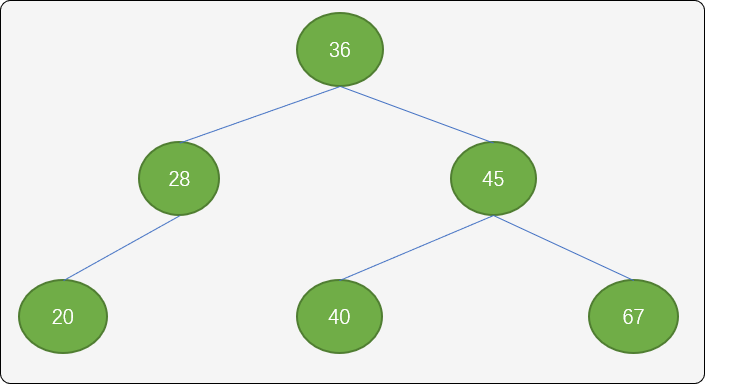
基于上面的树结构,查询任何一个结点的次数不会超过3 次。
稍调整一下数列中数字的顺序[20,28,36,40,45,67],由此构建出来的树结构会出现一边倒的现象,也增加了树的深度。

此棵树的深度为6,最多查询次数是6 次。在二叉排序树中,减少查找次数的最好办法,就是尽可能维护树左右子树之间的对称性,也就让其有平衡性。
所谓平衡二叉排序树,顾名思义,基于二叉排序树的基础之上,维护任一结点的左子树和右子树之间的深度之差不超过1。把二叉树上任一结点的左子树深度减去右子树深度的值称为该结点的平衡因子。
平衡因子只可能是:
0:左、右子树深度一样。1:左子树深度大于右子树。-1:左子树深度小于右子树。
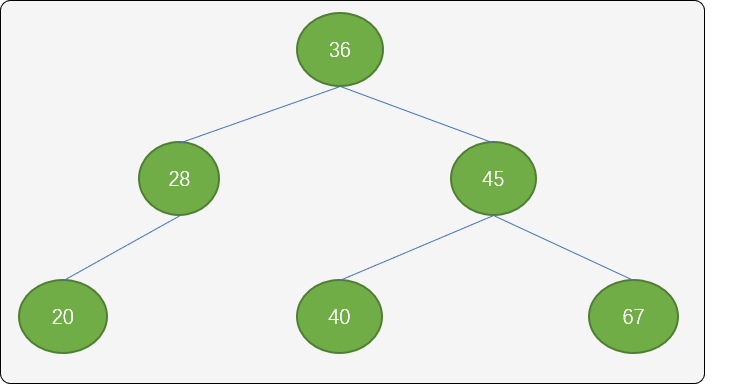
如下图,就是平衡二叉排序树,根结点的2 个子树深度相差为0, 结点28 的左、右子树深度为 1,结点45 的左右子树深度相差为0。
平衡二叉排序树相比较于二叉排序树,其API 多了保持平衡的算法。
3.1 二叉平衡排序树的数据结构
结点类:
''' 结点类 ''' class TreeNode: def __init__(self,value): self.value=value self.l_child=None self.r_child=None self.balance=0结点类中有4 个属性:
value:结点上附加的值。l_child:左子结点。r_child:右子结点。balance:平衡因子,默认平衡因子为0。
二叉平衡排序树类:
''' 树类 ''' class Tree: def __init__(self, value): self.root = None ''' LL型调整 ''' def ll_rotate(self, node): pass ''' RR 型调整 ''' def rr_rotate(self, node): pass ''' LR型调整 ''' def lr_rotate(self, node): pass ''' RL型调整 ''' def rl_rotate(self, node): pass ''' 插入新结点 ''' def insert(self, value): pass ''' 中序遍历 ''' def inorder_traversal(self, root): pass def is_empty(self): pass在插入或删除结点时,如果导致树结构发生了不平衡性,则需要调整让其达到平衡。这里的方案可以有4种。
LL型调整(顺时针):左边不平衡时,向右边旋转。
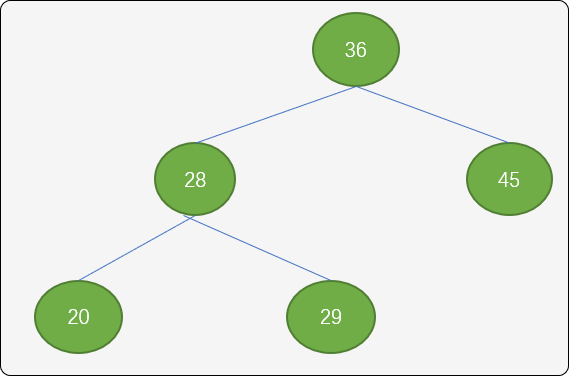
如上图,现在根结点36 的平衡因子为1。如果现插入值为18 结点,显然要作为结点20 的左子结点,才符合二叉排序树的有序性。但是破坏了根结点的平衡性。根结点的左子树深度变成3,右子树深度为1,平衡被打破,结点36 的平衡因子变成了2。
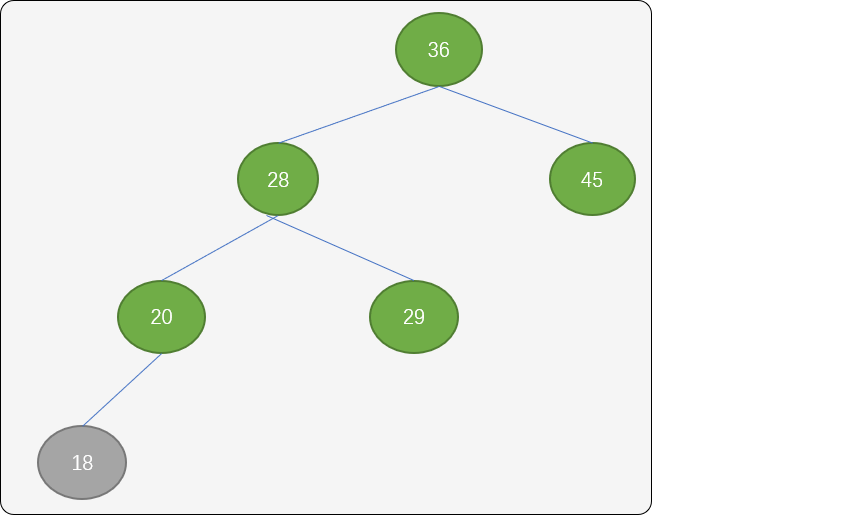
这里可以使用顺时针旋转方式,让其继续保持平衡,旋转流程:
- 让结点
28成为新根结点,结点36成为结点28的左子结点。 - 结点
29成为结点36的新左子结点。
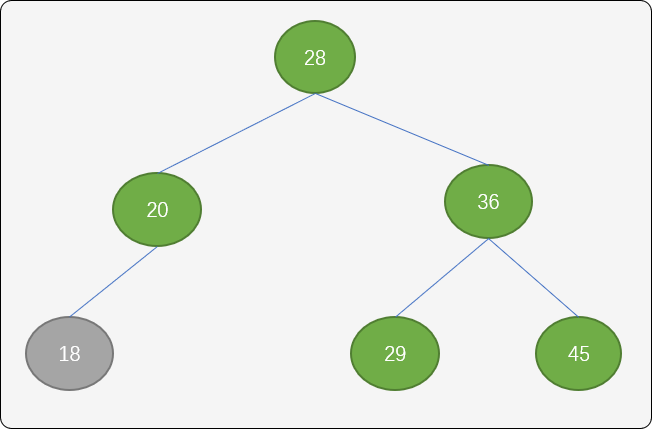
旋转后,树结构即满足了有序性,也满足了平衡性。
LL 旋转算法具体实现:
''' LL型调整 顺时针对调整 ''' def ll_rotate(self, p_root): # 原父结点的左子结点成为新父结点 new_p_root = p_root.l_child # 新父结点的右子结点成为原父结点的左子结点 p_root.l_child = new_p_root.r_child # 原父结点成为新父结点的右子结点 new_p_root.r_child = p_root # 重置平衡因子 p_root.balance = 0 new_p_root.balance = 0 return new_p_rootRR 型调整(逆时针旋转):RR旋转和LL旋转的算法差不多,只是当右边不平衡时,向左边旋转。
如下图所示,结点50 插入后,树的平衡性被打破。
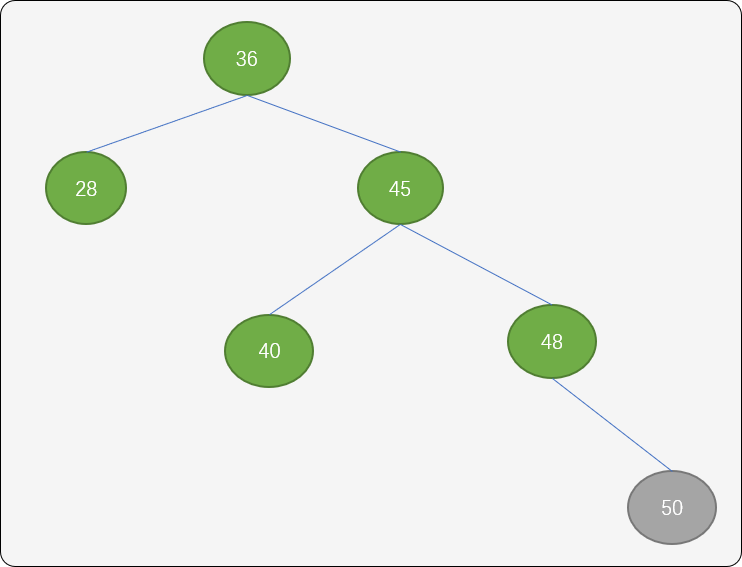
这里使用左旋转(逆时针)方案。结点36 成为结点45 的左子结点,结点45 原来的左子结点成为结点36的右子结点。
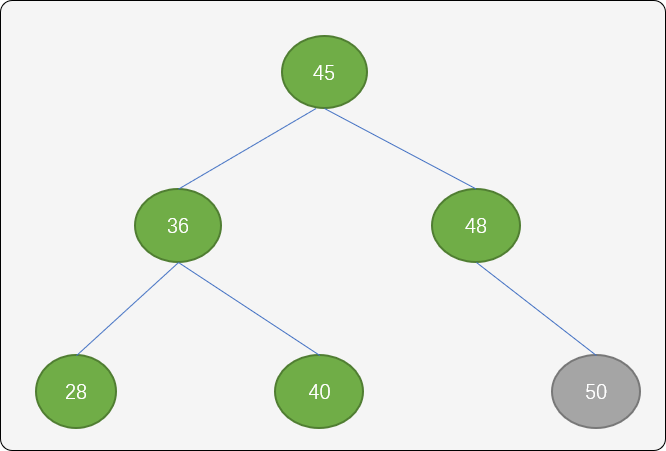
向逆时针旋转后,结点45的平衡因子为0,结点36的平衡因子为0,结点48 的平衡因子为-1。树的有序性和平衡性得到保持。
RR 旋转算法具体实现:
''' RR 型调整 ''' def rr_rotate(self, node): # 右子结点 new_p_node = p_node.r_child p_node.r_child = new_p_node.l_child new_p_node.l_child = p_node # 重置平衡因子 p_node.balance = 0 new_p_node.balance = 0 return new_p_nodeLR型调整(先逆后顺):如下图当插入结点28 后,结点36 的平衡因子变成2,则可以使用LR 旋转算法。
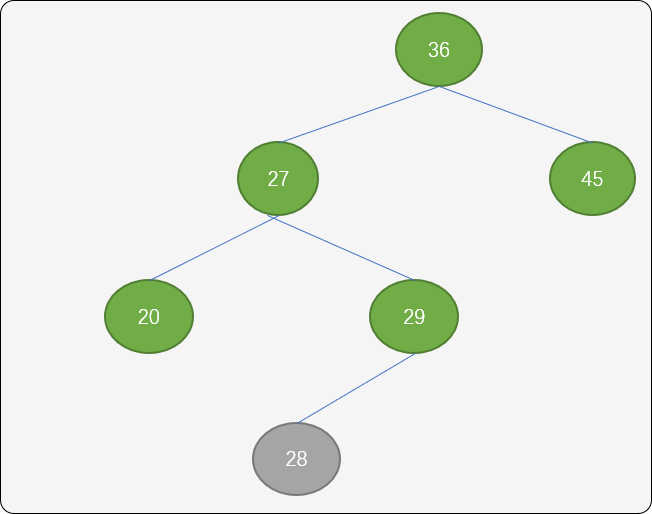
以结点29 作为新的根结点,结点27以结点29为旋转中心,逆时针旋转。
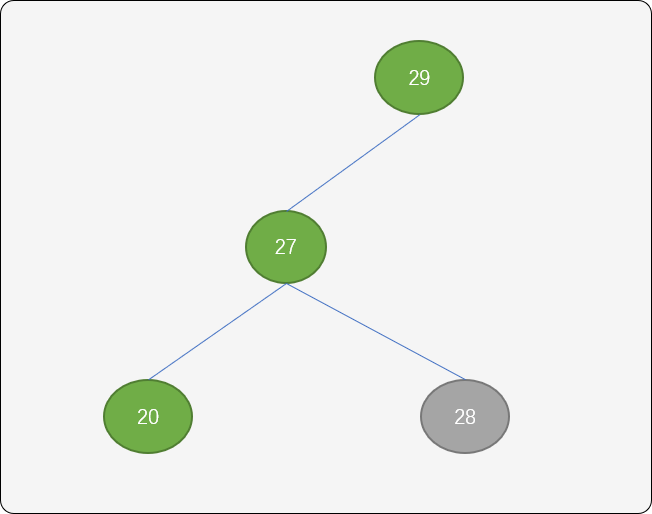
结点36以结点29为旋转中心向顺时针旋转。
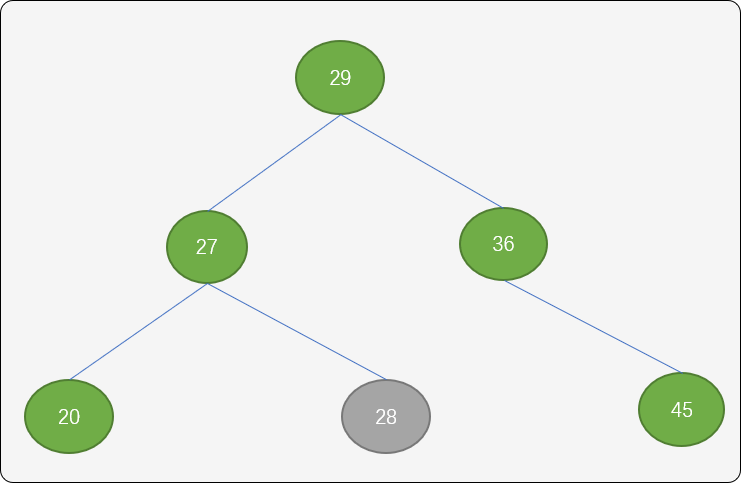
最后得到的树还是一棵二叉平衡排序树。
LR 旋转算法实现:
''' LR型调整 ''' def lr_rotate(self, p_node): # 左子结点 b = p_node.l_child new_p_node = b.r_child p_node.l_child = new_p_node.r_child b.r_child = new_p_node.l_child new_p_node.l_child = b new_p_node.r_child = p_node if new_p_node.balance == 1: p_node.balance = -1 b.balance = 0 elif new_p_node.balance == -1: p_node.balance = 0 b.balance = 1 else: p_node.balance = 0 b.balance = 0 new_p_node.balance = 0 return new_p_nodeRL型调整: 如下图插入结点39 后,整棵树的平衡打破,这时可以使用RL 旋转算法进行调整。
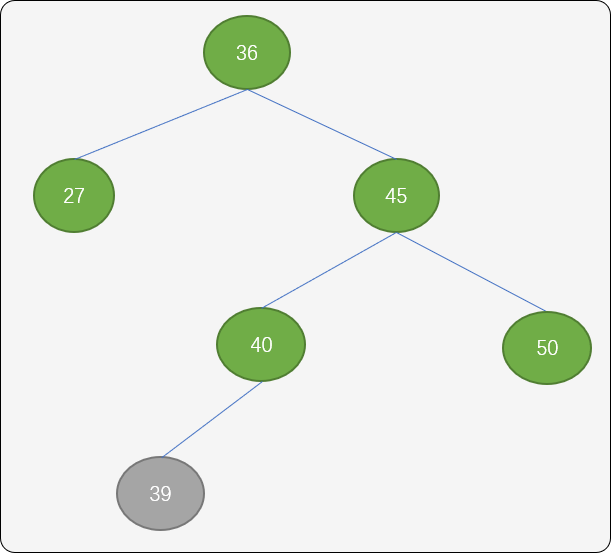
把结点40设置为新的根结点,结点45以结点40 为中心点顺时针旋转,结点36逆时针旋转。
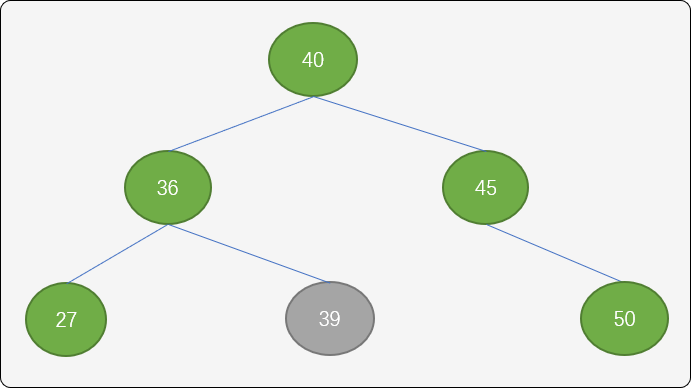
RL 算法具体实现:
''' RL型调整 ''' def rl_rotate(self, p_node): b = p_node.r_child new_p_node = b.l_child p_node.r_child = new_p_node.l_child b.l_child = new_p_node.r_child new_p_node.l_child = p_node new_p_node.r_child = b if new_p_node.balance == 1: p_node.balance = 0 b.balance = -1 elif new_p_node.balance == -1: p_node.balance = 1 b.balance = 0 else: p_node.balance = 0 b.balance = 0 new_p_node.balance = 0 return new_p_node编写完上述算法后,就可以编写插入算法。在插入新结点时,检查是否破坏二叉平衡排序树的的平衡性,否则调用平衡算法。
当插入一个结点后,为了保持平衡,需要找到最小不平衡子树。
什么是最小不平衡子树?
指离插入结点最近,且平衡因子绝对值大于
1的结点为根结点构成的子树。
''' 插入新结点 ''' def insert(self, val): # 新的结点 new_node = TreeNode(val) if self.root is None: # 空树 self.root = new_node return # 记录离 s 最近的平衡因子不为 0 的结点。 min_b = self.root # f 指向 a 的父结点 f_node = None move_node = self.root f_move_node = None while move_node is not None: if move_node.value == new_node.value: # 结点已经存在 return if move_node.balance != 0: # 寻找最小不平衡子树 min_b = move_node f_node = f_move_node f_move_node = move_node if new_node.value < move_node.value: move_node = move_node.l_child else: move_node = move_node.r_child if new_node.value < f_move_node.value: f_move_node.l_child = new_node else: f_move_node.r_child = new_node move_node = min_b # 修改相关结点的平衡因子 while move_node != new_node: if new_node.value < move_node.value: move_node.balance += 1 move_node = move_node.l_child else: move_node.balance -= 1 move_node = move_node.r_child if min_b.balance > -2 and min_b.balance < 2: # 插入结点后没有破坏平衡性 return if min_b.balance == 2: b = min_b.l_child if b.balance == 1: move_node = self.ll_rotate(min_b) else: move_node = self.lr_rotate(min_b) else: b = min_b.r_child if b.balance == 1: move_node = self.rl_rotate(min_b) else: move_node = self.rr_rotate(min_b) if f_node is None: self.root = move_node elif f_node.l_child == min_b: f_node.l_child = move_node else: f_node.r_child = move_node中序遍历: 此方法为了验证树结构还是排序的。
''' 中序遍历 ''' def inorder_traversal(self, root): if root is None: return self.inorder_traversal(root.l_child) print(root.value, end="->") self.inorder_traversal(root.r_child)二叉平衡排序树本质还是二树排序树。如果使用中序遍历输出的数字是有序的。测试代码。
if __name__ == "__main__": nums = [3, 12, 8, 10, 9, 1, 7] tree = Tree(3) for i in range(1, len(nums)): tree.inster(nums[i]) # 中序遍历 tree.inorder_traversal(tree.root) ''' 输出结果 1->3->7->8->9->10->12-> '''4. 总结
利用二叉排序树的特性,可以实现动态查找。在添加、删除结点之后,理论上查找到某一个结点的时间复杂度与树的结点在树中的深度是相同的。
但是,在构建二叉排序树时,因原始数列中数字顺序的不同,则会影响二叉排序树的深度。
这里引用二叉平衡排序树,用来保持树的整体结构是平衡,方能保证查询的时间复杂度为Ologn(n 为结点的数量)。
热门文章
- 12月17日|最高速度22.2M/S,2024最新Hysteria2免费节点高速订阅链接,便宜机场推荐
- 泰国象岛有什么好玩的地方(泰国象岛有什么好玩的景点)
- 宠物领养网站源码(宠物领养网站app)
- 宠物领养文章怎么写(关于宠物领养的话术)
- 12月8日|最高速度21.2M/S,2024最新Hysteria2免费节点高速订阅链接,便宜机场推荐
- 动物疫苗的作用是什么呢英文翻译(动物疫苗的作用是什么呢英文翻译成中文)
- 兽药疫苗冷藏室温度(兽用疫苗冷藏温度)
- 延吉宠物医院电话 延吉宠物医院电话号码
- 2月6日|最高速度18.4M/S,2025最新Hysteria2免费节点高速订阅链接,便宜机场推荐
- 12月30日|最高速度20.9M/S,2024最新Hysteria2免费节点高速订阅链接,便宜机场推荐